Progressões Aritméticas
Chama-se sequência ou sucessão numérica, a qualquer conjunto ordenado de números reais ou complexos. Assim, por exemplo, o conjunto ordenado A = (3, 5, 7, 9, 11, ... , 35) é uma sequência cujo primeiro termo é 3, o segundo termo é 5, o terceiro termo é 7 e assim sucessivamente

Aplicações: Progressão Aritmética
Engenharia civil: Projeção de periodo para completar uma escavação de metro
Táxis: O preço do táxi varia conforme uma PA
Economia: Cálculo de juros e investimentos.
Natureza: A famosa sequência de Fibonacci.
Calendários: Os dias são uma PA de razão 1.

Chama-se sequência ou sucessão numérica, a qualquer conjunto ordenado de números reais ou complexos. Assim, por exemplo, o conjunto ordenado A = (3, 5, 7, 9, 11, ... , 35) é uma sequência cujo primeiro termo é 3, o segundo termo é 5, o terceiro termo é 7 e assim sucessivamente.
Uma sequência pode ser finita ou infinita.
O exemplo dado (conjunto A) é de uma sequência finita.
Já a sequência dos números pares P = (0, 2, 4, 6, 8, ...) é infinita.
Exercício resolvido:
Considere as seguintes sequências de números:
I. 3, 7, 11,...
II. 2, 6, 18,...
III. 2, 5, 10, 17,...
O número que continua cada uma das sequências na ordem dada deve ser respectivamente:
a) 15, 36 e 24
b) 15, 54 e 24
c) 15, 54 e 26
d) 17, 54 e 26
e) 17, 72 e 26
Observe que a sequência I tem razão igual a 4, pois, 3 ⟶ 7 ⟶ 11 ⟶ 15 “vai de 4 em 4” a razão da progressão é 4, ou a diferença entre 7 e 3 é igual a 4.
A sequência II não é uma PA, pois, a lei de formação se dá em fatores que são obtidos multiplicando os termos por três. Sendo assim: 2 ⟶ 6 ⟶ 18 ⟶ 54.
A sequência III não é uma PA, pois, a lei de formação se dá em somas de números ímpares distintos (+ 3, +5, +7, +9). Sendo assim: 2 ⟶ 5 ⟶ 10 ⟶ 17 ⟶ 26.

Conceito de Progressão Aritmética - PA
Chama-se Progressão Aritmética (PA) toda sequência numérica cujos termos a partir do segundo, são iguais ao anterior somado com um valor constante denominado razão.
Exemplos:
A = (1, 5, 9, 13, 17, 21, ... ) razão = 4 (PA crescente)
B = (3, 12, 21, 30, 39, 48, ... ) razão = 9 (PA crescente)
C = (5, 5, 5, 5, 5, 5, 5, ... ) razão = 0 (PA constante)
D = (100, 90, 80, 70, 60, 50, ... ) razão = -10 (PA decrescente)
A diferença entre os termos é chamada de razão r.

Fórmula do enésimo termo
Pela definição de PA, a fórmula do segundo termo é:
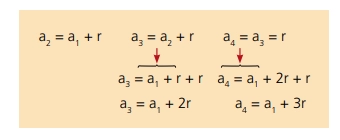
Logo se pode deduzir que para um termo qualquer ax:
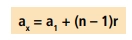

Importante
A lei de formação, ou seja, a expressão matemática que relaciona entre si os termos da sequência é denominada termo geral ou generalização.
Exemplos de aplicação do termo geral de uma PA
Considere a sequência cujo termo geral (lei geral ou generalização) seja dado por an = 3n + 5, onde n é um número natural não nulo.
Observe que atribuindo valores para n, obteremos o termo an (enésimo termo) correspondente.
Assim, por exemplo, para n = 20, teremos:
an = 3.20 + 5 = 65, e portanto o vigésimo termo dessa sequência (a20) é igual a 65.
Prosseguindo com esse raciocínio, podemos escrever os demais termos da sequência “S” que seria:
S = (8, 11, 14, 17, 20, ... ).
Outro exemplo:
Seja por exemplo a sequência de termo geral an = n2 + 4n + 10, para n inteiro e positivo.
Nestas condições, podemos concluir que a sequência poderá ser escrita como:
(15, 22, 31, 42, 55, 70, ... ).
Pela lei geral de formação:
a6 = 70 porque a6 = 62 + 4.6 + 10 = 36 + 24 + 10 = 70.

Propriedades das Progressões
Numa PA, cada termo (a partir do segundo) é a média aritmética dos termos equidistantes deste.
Exemplo:
Seja uma PA representada por três termos: (m, n, r )
O termo n, é a média entre os “vizinhos”
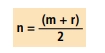

Numa PA, a soma dos termos equidistantes dos extremos é constante.
Exemplo geral:
Considere uma PA: (m, n, r, s, t); portanto, m + t = n + s = r + r = 2r
Exemplo prático:
Sabendo que a sequência (1 – 3x, x - 2, 2x + 1) é uma PA, determine o valor de X.
Pela propriedade a2 - a1 = a3 - a2
a1 = primeiro termo = 1-3x
a2 = segundo termo = x-2
a3 = terceiro termo = 2x+1
Resolvendo a equação

Soma dos n primeiros termos de uma PA
Seja a PA (a1, a2, a3, ..., an-1, an)
A soma dos n primeiros termos Sn = a1 + a2 + a3 + ... + an-1 + an , pode ser deduzida facilmente, da aplicação da segunda propriedade acima.
Temos:
Sn = a1 + a2 + a3 + ... + an-1 + an
É claro que também poderemos escrever a igualdade acima como:
Sn = an + an-1 + ... + a3 + a2 + a1
Somando membro a membro estas duas igualdades, vem:
2 vezes Sn = (a1 + an ) + (a2 + an-1) + ... + (an + a1 )
Logo, pela segunda propriedade acima, as n parcelas entre parênteses possuem o mesmo valor (são iguais à soma dos termos extremos a1 + an ), de onde concluímos que:
2 x Sn = (a1 + an).n , onde n é o número de termos da PA. Daí:

Exemplo:
Calcule a soma dos 200 primeiros números ímpares positivos.
Temos a PA: (1, 3, 5, 7, 9, ... )
Precisamos conhecer o valor de a200 .
Mas, a200 = a1 + (200 - 1).r = 1 + 199.2 = 399
Logo, Sn = [(1 + 399). 200]/2 = 40.000
Portanto, a soma dos duzentos primeiros números ímpares positivos é igual a 40.000.
Resumo
Nesta aula vimos um tipo específico de progressão, a PA. Progressão Aritmética é toda sequência de números na qual a diferença entre um termo e outro é constante. Essa diferença é chamada de razão, e costuma ser representada pela letra r.
Lista Geral de Questões
Referências:
JUNIOR, Roberto José Medeiros. Matemática II . Curitiba-PR: - e-Tec Brasil, 2011.