Equações do Primeiro Grau

A palavra "equação" tem como significado as palavras igualdade e equilíbrio.

Na equação nós buscamos encontrar o valor equivalente. Se em uma balança existem 3 kg de laranja e 1kg de maçã e do outro lado 2kg de laranja e 2 kg de limões, então teremos.

3 + 1 = 2 + 2

Perceba que apesar de valor diferente, o resultado é 4 em ambos os lados, logo são equivalentes, e atingem a igualdade ou equilíbrio.

Resolvendo equações de maneira prática

As equações podem ser resolvidas seguindo todas as regras ou de maneira mais prática como veremos a seguir.

Exemplo 1:

2x-6=0

Se atente ao fato de que procuramos um ponto de equilíbrio onde queremos descobrir qual o valor que ao multiplicar por 2, subtrair pelo 6 o resultado é o nosso zero.

Passo 1: Separar que não tem letra de quem tem.

Passo 2: Passar 0 para outro lado com o sinal inverso.

2x = 0+6

Passo 3: Realizar a soma.

2x = 6

Passo 4: Isolar o x, e dividir os dois lados da equação pelo mesmo termo.

x = 6 / 2

Passo 5: Fazer a divisão.

x = 3

Isso significa que:

2.3-6=0

Confira mais exemplos

Exemplo 2:

7x + 12 = 0

7x = 0 - 12

7x = -12

x = -12 / 7

x = $\frac{\mathrm{-12}}{7}$

Exemplo 3:

7x - 6 = -3x + 8

7x + 3x - 6 = + 8

7x + 3x = 8 +6

10x = 14

x = 14/10

x = 7/5 ou 1,4

Propriedade Distributiva

Na propriedade distributiva vamos multiplicar o primeiro fator, pela soma no parêntese.

Exemplo 1:

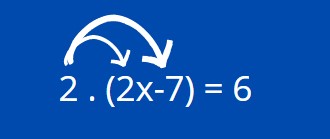
2 . (2x -7) = 6

Primeiro vamos multiplicar o 2 por 2x e -7.

4x - 14 = 6

agora seguir normalmente com nossa equação.

4x = 6 + 14

4x = 20

x = 20/4

x = 5

Exemplo 2:

2 x -3 . (4 - x) = 5 + 4 . (2x + 1)

No segundo caso vamos multiplicar o -3 por 4 e -x de um lado, e o 4 vezes 2x + 1. Depois vamos isolar quem tem x de uma lado, e que não tem de outro. Sempre invertendo o sinal ao passar o valor para o outro lado.

2x - 12 + 3x = 5 + 8x + 4

2x + 3x - 8x = 5 + 9 + 12

5x - 8x = 21

-3x = 21

x = 21/-3

x = -7

Aprenda Mais - Propriedade Distributiva

Equação do Primeiro Grau com Frações

$\frac{\mathrm{x}}{2}$+ $\frac{\mathrm{x}}{3}$- $\frac{\mathrm{x}}{4}$ = 14

1. Primeiro vamos tirar o MMC de 2, 3 e 4 = 12

2. Depois vamos dividir o resultado do MMC pelo denominador (parte inferior da fração), e depois multiplicar o denominador pelo numerador (número na parte de cima).

Ex: 12/2 = 6 | 6.x = 6x etc

$\frac{\mathrm{6x}}{12}$ + $\frac{\mathrm{4x}}{12}$ - $\frac{\mathrm{3x}}{12}$ = 168

3. Eliminar os denominadores

6x + 4x - 3x = 168

4. Fazer as operações

7x = 168

x$\frac{\mathrm{168}}{7}$

x = 24

Aprenda Mais - Equação do Primeiro Grau com Frações

Ferramentas

Muitas vezes você não entende como resolver uma equação, ou não encontra a sua explicação na internet, então a nossa sugestão é usar o site ou aplicativo do Math Solver da Microsoft. Basta enviar uma foto, escanear ou digitar a equação que o programa te ensina o passo a passo de como obter a resolução. Obs: Existem outros aplicativos que fazem a mesma coisa.

Site do Math Solver

Aplicativo para Android

Aplicativo para iOS

Questões Resolvidas

Aprenda Mais - Questões Resolvidas

Lista Geral de Questões

Equação do Primeiro Grau