Equações do Segundo Grau

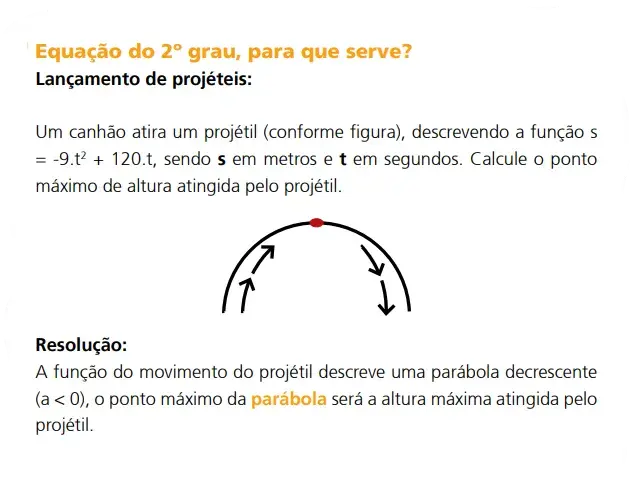
Aplicações: Equação do 2º grau

Movimento de um projétil: Encontrar a altura máxima atingida

Física: Análise dos movimentos uniformemente variados (MUV), Lei da Queda dos Corpos

Uma equação quadrática ou equação do segundo grau é uma equação polinomial de grau dois.

A forma geral deste tipo de equação é: ax2 + bx + c = 0, onde x é uma variável, e a, b e c são constantes, das quais a ≠ 0 (caso contrário, a equação torna-se linear). As constantes a, b e c, são chamadas respectivamente de coeficiente quadrático, coeficiente linear ou termo independente.

Resumindo:

Forma geral: ax² + bx + c = 0

Onde a, b, c pertencem (∈) ao conjunto dos números Reais, com a ≠ 0.

Desta forma, são equações do segundo grau com uma variável:

a) 2x² – 3x + 4 = 0

Onde: a = 2 | b = - 3 | c = 4

b) 2y² + 8y – 14 = 0

Onde: a = 2 | b = 8 | c = -14

Resolução de equações de 2º grau – cálculo das raízes reais

Talvez o método mais conhecido no Brasil para encontrar as raízes (solução) de uma equação do 2º grau seja a fórmula de Bháskara.

Neste caso – da resolução das equações de 2º grau –, somente um livro diz que a fórmula de Bháskara não é dele: “só temos a contar mais uma coisinha: a fórmula de Bháskara, curiosamente, não foi deduzida por Bháskara.

Como já dissemos, a fórmula de Bháskara não foi proposta por Bháskara. E não se sabe por que a fórmula acabou sendo batizada com seu nome. Alias, diga-se de passagem, esse não é o único caso em que se atribui uma descoberta a alguém que não a realizou. Bháskara viveu na Índia por volta de 1150. Esse ilustre matemático resolveu vários problemas complicados, alguns dos quais envolviam equações de 2º grau.

No entanto, muito antes dele, a resolução da equação já era conhecida. Os historiadores encontraram indícios de que, na civilização da babilônia, em 1700 a.C., já eram resolvidas algumas equações de 2º grau. Depois dessa época remota, parece ter sido Al-Khowarizmi, no século IX, o maior especialista no assunto.

Ele viveu em Bagdá e é considerado um dos principais criadores da álgebra. Escreveu o livro Al-jabr we muqabalah, cujo título inspirou o nome dado a essa ciência. Nessa obra, Al-Khowarizmi apresentou exemplos de como resolver equações de 2º grau. O interessante é que ele não usava fórmulas, nem símbolos algébricos. Ele trabalhava com palavras e figuras!”

Retirado de: http://antiga.ppgect.ufsc.br/dis/17/Dissert.pdf

Al-Khowarizmi: Autor do livro Al-jabr we muqabalah

Uma equação de 2º grau tem três termos principais

1. O termo que possui a variável ao quadrado (representado pela letra ‘a’)

2. A variável (está ao lado do ‘x’, representado pela letra ‘b’)

3. O termo independente (representado pela letra ‘c’).

A fórmula geral é representada por: ax2 + bx + c = 0

Se ‘a’ for igual a zero, teremos uma equação do 1o grau, logo - para ser uma equação do 2o grau - o coeficiente ‘a’ não pode ser igual a zero.

Na equação:

- 34a² + 28a - 32 = 0 tem-se:

a = - 34 | b = 28 | c = - 32

E na equação 10x - 3x² = 32 +15x²?

Neste caso temos que transformar a equação que está “desarrumada” na equação, na forma geral:

Subtraindo 32 de ambos os lados:

10x - 3x² - 32 = 32 +15x² - 32

10x - 3x² - 32 = 15x²

Subtraindo 15x² em ambos os termos:

10x - 3x² - 32 - 15x² = 15x² - 15x²

10x - 3x² - 32 - 15x² = 0

Somando-se os termos em comum:

10x - 32 - 18x² = 0

Colocando em ordem de maior para o menor expoente:

- 18x² + 10x - 32 = 0

Agora é intuitivo determinar os coeficientes:

a = -18 | b= +10 | c = -32

Através da equação do 2º grau é possível descobrir a altura máxima atingida por um projétil.

Fórmula geral de resolução de equações de 2° grau

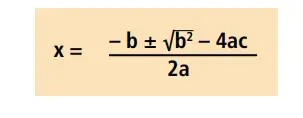
Deste modo, justificamos a presença do sinal de ± para representar as duas soluções da equação do 2º grau, a de discriminante positivo e negativo.

Outro modo de apresentar a Fórmula de Bháskara é separar a equação da parte de dentro da raiz (radicando), que é chamada de "DISCRIMINANTE" e representada pela letra grega Δ (delta).

Portanto, a fórmula de Bháskara pode ser escrita assim:

Onde "a", "b" e "c" são os coeficientes dos termos de nossa função quadrática.

Nesta aula vamos estudar a vantagem analítica deste "delta" na fórmula.

Se o delta for igual à zero (Δ = 0), não teremos diferença entre as raízes.

Como uma função quadrática sempre tem que ter duas raízes, dizemos que a função com Δ = 0 tem as duas raízes idênticas.

Se Δ ≠ 0, então a função tem duas raízes distintas:

Agora, quando Δ ≠ 0 (raízes distintas), teremos duas situações:

Δ for positivo (Δ > 0)

Δ for negativo (Δ < 0)

Como o Δ é um radicando (está dentro de uma raiz quadrada), se for negativo (Δ < 0), as raízes serão números complexos não reais, pois raiz de número negativo não é real. E quando Δ for positivo (Δ > 0), então as raízes serão números REAIS.

Algumas considerações importantes sobre a fórmula de Bháskara: O hábito de dar nome de Bháskara para a fórmula de resolução da equação de 2º grau se estabeleceu no Brasil por volta de 1960. Esse costume, aparentemente só brasileiro (não se encontra o nome de Bháskara para essa fórmula na literatura internacional), não é adequado, pois os problemas que recaem numa equação de 2º grau já apareciam quase 4000 anos atrás, em textos escritos pelos babilônicos.

Nestes textos, o que se tinha era uma receita (escrita em prosa, sem uso de símbolos) que ensinava como proceder para determinar as raízes em exemplos concretos com coeficientes numéricos.

Bháskara que nasceu na Índia em 1114 e viveu até cerca de 1185; foi um dos mais importantes matemáticos do século 12. As duas coleções de seus trabalhos mais conhecidas são Lilavati ("bela") e Vijaganita ("extração de raízes"), que tratam de aritmética e álgebra respectivamente, e contêm numerosos problemas sobre equações de lineares e quadráticas (resolvidas também com receitas em prosa) progressões aritméticas e geométricas, radicais, tríadas pitagóricas e outros.

Até o fim do século 16 não se usava uma fórmula para obter as raízes de uma equação do 2º grau, simplesmente porque não se representavam por letras os coeficientes de uma equação. Isso só começou a ser feito a partir de François Viéte, matemático francês que viveu de 1540 a 1603.

Embora não se deva negar a importância e a riqueza da obra de Bháskara, não é correto atribuir a ele a conhecida fórmula de resolução da equação de 2º grau.

Fonte: Revista do Professor de Matemática, SBM - nº 39

Exercícios resolvidos:

Lista Geral de Questões

Equação do 2º grau